B+树实现

​ 最近看八股不时会看到B+树这个概念，想起之前做的CMU15445在Project2中就有这方面的实现，但我当时做的2021的，Project2是Hash Index，实现了一个可扩展的哈希表。但在2021的项目下还是保留了之前的代码和测试用例，所以我就想折磨锻炼一下自己。

​ 附：B+ Tree Visualization可视化

​ 以下分阶段阐述实现过程吧，首先是B+树结构，插入流程（包括Split），删除流程（包括Coalesce，redistribute），并发保证。

​ 实现代码主要在/include/storage/index 和 include/storage/page和对应的cpp文件中。

1 B+树结构

​ 该lab的B+树我觉得构造的挺好的，将B+树的节点分为了内部节点，叶子节点，使用OOP的思想来使用。以下标题均省略b_plus_tree前缀

1.1 page

​ 这是leaf page和internal_page都继承的父类，里面包含一些共用的字段和方法。

IndexPageType page_type_;	// internal or leaf
lsn_t lsn_;	// 序列号，用于project 4？
int size_;	// key value 的 个数
int max_size_; // 最大个数
page_id_t parent_page_id_; 
page_id_t page_id_;

1.2 internal_page

​ 内部节点：主要存储有序的m个key和m+1个指针，第一个键被设置为无效。刚开始我还有点奇怪指针是咋存放的，因为MappingType array_[0];我感觉是用来存值kv的，而由于ValueType是泛型，所以是可以用于存储子页的id的。

1.3 leaf_page

​ 叶子节点：存储实际数据，也就是kv对，并且含有一个指针指向下一个page。

1.4 b_plus_tree

​ B+树的具体实现

std::string index_name_;
page_id_t root_page_id_;
BufferPoolManager *buffer_pool_manager_;
KeyComparator comparator_;
int leaf_max_size_;
int internal_max_size_;

2 插入流程

​ 要通过b_plus_tree_insert_test.cpp的测试用例，就要实现插入和查询两个操作，这里写说说插入吧。

2.1 插入

​ 首先判断树是否为空，如果是空的，则需要创建一颗新树，不是则直接插入值

bool BPLUSTREE_TYPE::Insert(const KeyType &key, const ValueType &value, Transaction *transaction) {
  if (IsEmpty()) {
    StartNewTree(key, value);
    return true;
  }
  bool ret = InsertIntoLeaf(key, value, transaction);
  return ret;
}

​ 建立新树的流程，从bpm获取一个新页用于构造leafpage，然后初始化root page，注意unpin和更新header record。

void BPLUSTREE_TYPE::StartNewTree(const KeyType &key, const ValueType &value) {
  // 1. 创建一个newPage
  page_id_t new_page_id = INVALID_PAGE_ID;
  Page *root_page = buffer_pool_manager_->NewPage(&new_page_id);
  assert(root_page != nullptr);
  LeafPage *root = reinterpret_cast<LeafPage *>(root_page->GetData());
  // 2. 修改root page id
  root->Init(new_page_id, INVALID_PAGE_ID, leaf_max_size_);
  root_page_id_ = new_page_id;
  UpdateRootPageId(1);  // 更改root page id时记得调用该函数
  // 3. 插入
  root->Insert(key, value, comparator_);
  // 4. 注意new page的pin_count=1，之后记得unpin page
  buffer_pool_manager_->UnpinPage(new_page_id, true);
}

​ 插入数据到leaf page，首先要找到该key所在的leaf_page（不是指该key已经存在）。如果重复直接返回即可，如果插入后的size大于该leaf_page的maxsize，则要分裂并修改parent page的信息

bool BPLUSTREE_TYPE::InsertIntoLeaf(const KeyType &key, const ValueType &value, Transaction *transaction) {
  // 1. 找到叶子page
  Page* page = FindLeafPage(key, false, false);
  LeafPage* leaf_page = reinterpret_cast<LeafPage*>(page->GetData());
  // 2. 插入key-value，并根据size判断是否该key是否存在
  int old_size = leaf_page->GetSize();
  int new_size = leaf_page->Insert(key, value, comparator_);
  if (new_size == old_size) { // lab要求插入重复key时直接返回false即可
    buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), false);
    return false;
  }
  // 3. 如果size大于maxsize，则要split了
  if (new_size > leaf_page->GetMaxSize()) {
    LeafPage *new_leaf_page = Split(leaf_page);
    InsertIntoParent(leaf_page, new_leaf_page->KeyAt(0), new_leaf_page, transaction);
    buffer_pool_manager_->UnpinPage(new_leaf_page->GetPageId(), true);
  }
  buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), true);
  return true;
}

​ Split的流程是：申请一个新page，如果是leaf page的话，需要调整leaf page的指向，然后迁移一部分数据（实现leaf_page的MoveHalfTo函数，其实就是数组的拆分，可以调用std::copy）；如果是internal page的话，只需要迁移数据即可，但调用CopyNFrom时记得设置其leaf_page的parent_id为新page的id。

N *BPLUSTREE_TYPE::Split(N *node) {
  page_id_t new_page_id = INVALID_PAGE_ID;
  Page* new_page = buffer_pool_manager_->NewPage(&new_page_id); // 申请一个新页
  N* new_node = reinterpret_cast<N *>(new_page->GetData());
  if (node->IsLeafPage()) { // 如果是叶子节点
    LeafPage *old_leaf_page = reinterpret_cast<LeafPage *>(node);
    LeafPage *new_leaf_page = reinterpret_cast<LeafPage *>(new_node);
    // new_page 和 old_page 的 parent_id是一样的
    new_leaf_page->Init(new_page_id, old_leaf_page->GetParentPageId(), leaf_max_size_);
    old_leaf_page->MoveHalfTo(new_leaf_page);   // 移动old至new
    // 调整指针指向
    new_leaf_page->SetNextPageId(old_leaf_page->GetNextPageId());
    old_leaf_page->SetNextPageId(new_leaf_page->GetPageId());
    new_node = reinterpret_cast<N *>(new_leaf_page);  // 记得转化
  } else { // 如果是内部节点
    InternalPage *old_internal_page = reinterpret_cast<InternalPage *>(node);
    InternalPage *new_internal_page = reinterpret_cast<InternalPage *>(new_node);

    new_internal_page->Init(new_page_id, old_internal_page->GetParentPageId(), internal_max_size_);
    old_internal_page->MoveHalfTo(new_internal_page, buffer_pool_manager_);
    new_node = reinterpret_cast<N *>(new_internal_page);
  }
  return new_node;
}

​ InsertIntoParent主要是修改父页的指针指向，如果old_node是根节点，则要增加一层（那不是就不会增加？注意，这是一个递归方法，如果下层都满了，会递归到上层直到遇到根节点，增加层高）

void BPLUSTREE_TYPE::InsertIntoParent(BPlusTreePage *old_node, const KeyType &key, BPlusTreePage *new_node,
                                      Transaction *transaction) {
  // 1. old_node是根节点，整棵树会升高一层
  if (old_node->IsRootPage()) {
    // 新增一个新page
    page_id_t new_page_id = INVALID_PAGE_ID;
    Page* new_page = buffer_pool_manager_->NewPage(&new_page_id);
    root_page_id_ = new_page_id;

    InternalPage *new_root_page = reinterpret_cast<InternalPage *>(new_page->GetData());
    new_root_page->Init(new_page_id, INVALID_PAGE_ID, internal_max_size_);
    // 修改新的根节点的孩子指针
    new_root_page->PopulateNewRoot(old_node->GetPageId(), key, new_node->GetPageId());
    // 修改old_node 和 new_node的父指针
    old_node->SetParentPageId(root_page_id_);
    new_node->SetParentPageId(root_page_id_);
    UpdateRootPageId();
    buffer_pool_manager_->UnpinPage(new_page->GetPageId(), true);
    return ;
  }
  // 2. old_node不是根节点
  Page* parent_page = buffer_pool_manager_->FetchPage(old_node->GetParentPageId());
  InternalPage* internal_parent_page = reinterpret_cast<InternalPage *>(parent_page->GetData());
  internal_parent_page->InsertNodeAfter(old_node->GetPageId(), key, new_node->GetPageId());
  // 父节点满了
  if (internal_parent_page->GetSize() > internal_parent_page->GetMaxSize()) {
    InternalPage* new_parent_page = Split(internal_parent_page);
    InsertIntoParent(internal_parent_page, new_parent_page->KeyAt(0), new_parent_page, transaction);
    // 这里要注意unpin拆分后的新节点
    buffer_pool_manager_->UnpinPage(new_parent_page->GetPageId(), true);
  }
  buffer_pool_manager_->UnpinPage(parent_page->GetPageId(), true);
}

​ 实现这些函数插入整体流程就差不多明白了，其他的函数都比较简单，就不贴出来了。

2.2 查询

​ 查询的流程很简单，找到key对应的leaf_page，在使用leaf_page的Lookup函数找到对应kv值即可。

bool BPLUSTREE_TYPE::GetValue(const KeyType &key, std::vector<ValueType> *result, Transaction *transaction) {
  // 1. 找到叶子的page
  Page *page_ptr = FindLeafPage(key, false, false);
  B_PLUS_TREE_LEAF_PAGE_TYPE* leaf_ptr = reinterpret_cast<B_PLUS_TREE_LEAF_PAGE_TYPE*>(page_ptr->GetData());
  // 2. 在叶子page找到该key
  ValueType value{};
  bool ret = leaf_ptr->Lookup(key, &value, comparator_);
  // 3. unpin 该页
  buffer_pool_manager_->UnpinPage(page_ptr->GetPageId(), false);
  if (!ret) {
    return false;
  }
  result->push_back(value);
  return true;
}

​ 实现了这些还没完，要想跑通测试用例，还需要实现IndexIterator的迭代器。

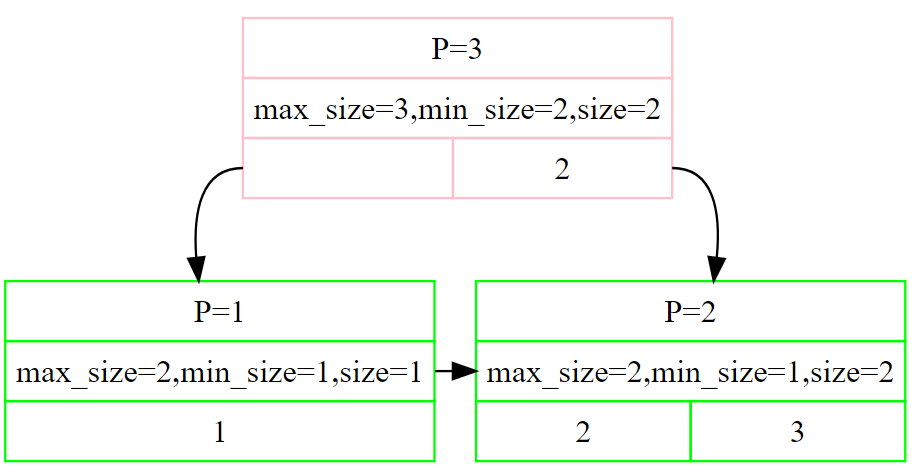
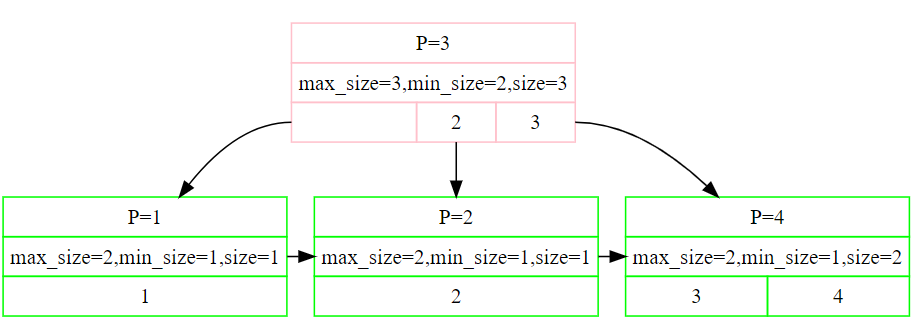
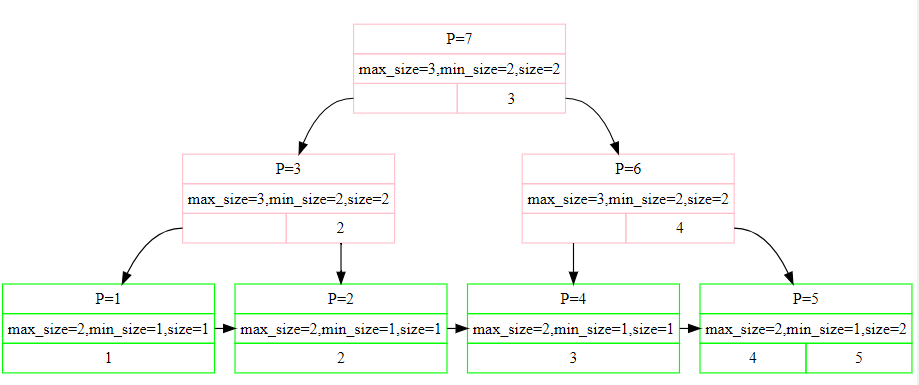
添个使用lab测试print的图片

3 删除流程

4 并发保证

参考

Project #2 - B+Tree | CMU 15-445/645 :: Intro to Database Systems (Fall 2020)

CMU 15445 Project 2A 实现并发B+树的数据库索引（查询和插入） - 简书 (jianshu.com)

《数据库系统概念》